Introduction
本文是对EDU2D-Airfoil-Spline代码的阅读总结。主要包含两项内容。一是三次样条插值。而是求解三对角线性方程组。
参考网址:
目的:输入翼型数据点,通过三次样条插值,得到加密后的翼型。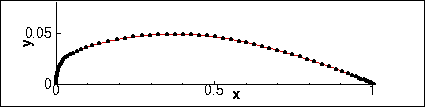
Piecewise cubic polynomial interpolation
三次样条多项式
有坐标点
$$
\begin{array}{l}
x: & x_1 & < & x_2 & < & \cdots & < & x_n\\
y: & y_1 & & y_2 & & \cdots & & y_n
\end{array}
$$
在区间$x_i,x_{i+1}$上有:
$$
S_i(x)=a_i + b_i (x-x_i) +c_i(x-x_i)^2 +d_i(x-x_i)^3,\quad i=1,2,\cdots,ns-1
$$
其中$a_i,b_i,c_i,d_i$代表$4(n-1)$个待求系数,使其满足:
- 同一点两侧插值的连续性:
$$
S_i(x_i)=y_i,\\
S_i(x_{i+1})=y_{i+1}
$$ - 同一点两侧插值的一阶及二阶微分的连续性:
$$
S^{‘}_i(x_{i+1})=S^{‘}_{i+1}(x_{i+1})\\
S^{‘’}_i(x_{i+1})=S^{‘’}_{i+1}(x_{i+1})
$$
样条函数及其微分为:
$$\left\{ \begin{array}{lllllllll}
S_i(x)&=& a_i &+& b_i (x-x_i) &+& c_i(x-x_i)^2 &+& d_i(x-x_i)^3\\
S^{‘}_i(x)&=& & & b_i &+& 2c_i(x-x_i) &+& 3d_i(x-x_i)^2\\
S^{‘’}_i(x)&=& & & & & 2c_i &+& 6d_i(x-x_i)
\end{array}\right.
$$
设步长$h_i=x_{i+1}-x_i$,根据上边条件:
$$\left\{ \begin{array}{ccccccccc}
a_i & & & & & & &=& y_i\\
a_i &+& b_i h_i &+& c_i h_i^2 &+& d_i h_i ^3 &=& y_{i+1}\\
& & b_i &+& 2c_i h_i &+& 3d_i h_i^2 &=& b_{i+1}\\
& & & & 2c_i &+& 6d_i h_i &=& 2c_{i+1}
\end{array}\right.
$$
写成:
$$\left\{ \begin{array}{ccc}
a_i &=& y_i\\
b_i &=& \dfrac{y_{i+1}-y_i}{h_i}- h_i c_i -\dfrac{h_i}{3}(c_{i+1}-c_i) \\
h_i c_i +2(h_i+h_{i_1}) c_{i+1} + h_{i+1} c_{i+2} &=& 3 (\dfrac{y_{i+2}-y_{i+1}}{h_{i+1}} - \dfrac{y_{i+1}-y_i}{h_i})\\
d_i &=& \dfrac{c_{i+1}-c_i}{3h_i}
\end{array}\right.
$$
通过求解关于$c_i$的三对角矩阵,进而得到样条函数的系数。
边界条件
自由边界(Natural)
$c_1=0,c_n=0$
方程组为:
$$
\pmatrix{1 & 0 & & & & \\
h_1& D_2 & h_2 & & & \\
& h_2 & D_3 & h_3 & & \\
& & \ddots &\ddots & \ddots & \\
& & & h_{n-2} & D_{n-1} & h_{n-1} \\
& & & & 0 & 1
}
\pmatrix{c_1\\
c_2\\
c_3\\
\vdots\\
c_{n-1}\\
c_n
}=
3\pmatrix{0\\
\frac{y_{3}-y_{2}}{h_{2}}- \frac{y_{2}-y_1}{h_1}\\
\frac{y_{4}-y_{3}}{h_{3}}- \frac{y_{3}-y_2}{h_2}\\
\frac{y_{5}-y_{4}}{h_{4}}- \frac{y_{4}-y_3}{h_3}\\
\vdots\\
\frac{y_{n}-y_{n-1}}{h_{n-1}}- \frac{y_{n-1}-y_{n-2}}{h_{n-2}}\\
0
}
$$
其中$D_i=2(h_{i-1}+h_i)$
固定边界(Clamped)
$$\left\{ \begin{array}{rcc}
S_1^{‘}(x_1) &=& A\\
S_{n-1}^{‘}(x_n) &=& B\\
\end{array}\right.
$$
可得
$$\left\{ \begin{array}{rcc}
2h_1c_1 + h_1 c_2 &=& 3(\dfrac{y_2-y_1}{h_1}-A)\\
h_{n-1}c_{n-1} + 2h_{n-1} c_n &=& 3(B-\dfrac{y_n-y_{n-1}}{h_{n-1}})
\end{array}\right.
$$
所以此时方程组为:
$$
\pmatrix{2h_1 & h_1 & & & & \\
h_1& D_2 & h_2 & & & \\
& h_2 & D_3 & h_3 & & \\
& & \ddots &\ddots & \ddots & \\
& & & h_{n-2} & D_{n-1} & h_{n-1} \\
& & & & h_{n-1} & 2h_{n-1}
}
\pmatrix{c_1\\
c_2\\
c_3\\
\vdots\\
c_{n-1}\\
c_n
}=
3\pmatrix{\frac{y_2-y_1}{h_1}-A\\
\frac{y_{3}-y_{2}}{h_{2}}- \frac{y_{2}-y_1}{h_1}\\
\frac{y_{4}-y_{3}}{h_{3}}- \frac{y_{3}-y_2}{h_2}\\
\frac{y_{5}-y_{4}}{h_{4}}- \frac{y_{4}-y_3}{h_3}\\
\vdots\\
\frac{y_{n}-y_{n-1}}{h_{n-1}}- \frac{y_{n-1}-y_{n-2}}{h_{n-2}}\\
B-\frac{y_n-y_{n-1}}{h_{n-1}}
}
$$
三对角方程组的求解
$$
\pmatrix{b_1& c_1 & & & \\
a_2& b_2 & c_2 & & \\
& a_3 & b_3 & \ddots & \\
& & \ddots& \ddots & c_{n-1}\\
& & & a_{n} & b_{n}
}
\pmatrix{x_1\\
x_2\\
x_3\\
\vdots\\
x_{n-1}\\
x_n
}=
\pmatrix{r_1\\
r_2\\
r_3\\
\vdots\\
r_{n-1}\\
r_n
}
$$
$$
c_i^{‘}=\left\{
\begin{array}{ll}
\frac{c_i}{b_i} &;i=1\\
\frac{c_i}{b_i-c_{i-1}^{‘}a_i}&;i=2,3,\cdots,n-1
\end{array}\right.
$$
$$
d_i^{‘}=\left\{
\begin{array}{ll}
\frac{d_i}{b_i} &;i=1\\
\frac{d_i-d_{i-1}^{‘}a_i}{b_i-c_{i-1}^{‘}a_i}&;i=2,3,\cdots,n-1
\end{array}\right.
$$
$$
x_i=d_i^{‘}-c_i^{‘}x_{i+1} \quad; i=n-1,n-2,\cdots,1
$$