When I was a undergraduate, I was luck enough to watch MIT video lecture, Linear Algebra. Today I find this course extremely useful in the area of CFD. What benefit me a lot are a series of vedios of great interest, named The Essence of Linear Algebra.
I note down the understandings of linear algebra on a geometric level.
Introduction
There’s a fundamental difference between understanding linear algebra on a numerical level and understanding it on a geometric level.
The geometric understanding is what lets you judge what tools to use to solve specific problem, fell why they work, and know how to interpret the results.
And the numeric understanding is what lets you actually carry through the application of those tools.
Vectors. What even are they?
From the physics student’s perspective, vectors are arrows pointing in space. What defines a given vector is its length and the direction it’s pointing.
The computer science perspective is that vectors are ordered lists of numbers.
Form the mathematician’s perspective, vectors can be anything where there’s a sensible notion of adding two vectors and multiplying a vector by a number.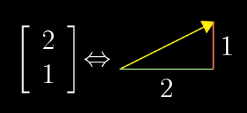
The rest part of the chapter is about understanding adding and multiplying operations with Geometric approach instead of digits, which are too simple to write down.
Linear combinations, span, and bases
The bases of a vector space are a set of linearly independent vectors that span the full space.
For example, any vector in a plane can be obtained by the combination of two independent vectors. The two independent vectors are called bases of the space.
Matrices as Linear transformations
Transformations are functions with vectors as inputs and vectors as outputs. For linear transformations, all lines remain lines and the origin must remain fixed in place. We can think about them visually as smooshing around space in such a way that the grid lines stay parallel and evenly spaced, and so that the origin remains fixed.
What are Matrices?
After a transformation, the base i vector turns into (a,c), the base j vector turns into (b,d). This means each column of a matric record the transformation of each base. In another word, a matric represents a transformation.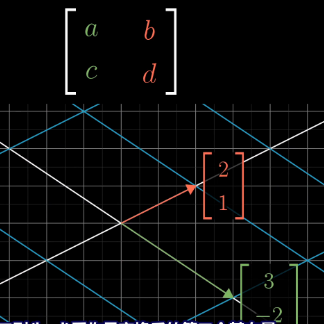
When apply a transformation to a vector, you get a new vector.
This is defined as matric-vector multiplication.
Matrix multiplication as composition
Multiplying two matrices has the geometric meaning of applying one transformation the another.
The determinant
The determinant of a transformation tells how much a transformation scales things(area in 2D, volume in 3D).
Inverse matrices, column space, rank, and null space
Each linear equation system has some kind of linear transformation associated with it. When the transformation has an inverse, you can use the inverse to solve the system.
Column space is the all possible linear combinations of the column vector of a matric, which lets us understand when a solution even exists.
The column rank of A is the dimension of the column space of A.
Null space is the set of all possible solutions which are turned into zero vector when applied a transformation.
Non-square matrix
Non-square matrices represent transformations between different dimensions.
Dot products
Taking a dot product with a unit vector can be interpreted as projecting a vector onto the span of that unit vector and taking the length. Under this circumstance, a vector can be understood as a projection matrix, or a projection transformation.
Cross products
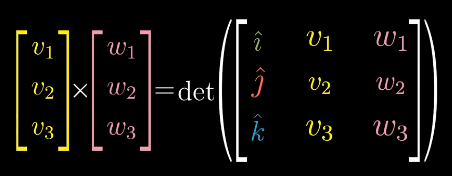
Cross products equal to the determinant of the matrix with those coordinates as columns. Their orientation are determined using the right hand rule.
Change of basis
How to translate the description of individual vectors back and forth between coordinate systems?
The matrix, whose columns represent the new basis vectors but written in old coordinates, can be thought as a transformation recording where the basis landing. The matrix translates vectors in new coordinate to old one.
Space itself has no intrinsic grid.
Eigenvectors and eigenvalues
$$Av=\lambda v$$
Eigenvectors are the special vectors staying on its own span during the transformation. And each eigenvector has associated eigenvalue with it. Eigenvalue is just the factor by which the eigenvector stretched or squashed during the transformation.
Last but not least
I find the $\pi$ creature very interesting. So I use it as my new WeChat avatar.
There are a lot of tricks in the area of CFD if we rethink on a geometric level. For example, in a finite-volume code, we can write just a subroutine to solve the split three-Dimensional Riemann problem, and then use the rotation matrix and its inverse to comepute the interface flux. For another example, when treat slip boundary condition, it’s tedious to set the normal velocity in the ghost cell opposite sign to that in the inner cell, and set the tangential velocity same sign. If we use a mirror matrix, things can be much easier. I will write down some tricks if I find time.