摘要
高温气体统计热力学将组分$s$的内能分为平动能、旋转能、振动能和电子能。其中平动振动过程的特征时间尺度远小于其他时间尺度,可以认为处于平衡状态,用一个平动旋转温度$T^{tr}$表征。
此外也可以用拟合曲线得到组分的定压比热和内能。
Model 1
对于单原子分子:
$$e_s=\frac{3}{2}R_s T^{tr} + e^{el}_s + e^0_s$$
对于双原子分子:
$$e_s=\frac{5}{2}R_s T^{tr} + e^{v}_s+ e^{el}_s + e^0_s$$
其中$e^{v}_s, e^{el}_s, e^0_s$分别是组分$s$的振动能、电子能和零点能(生成焓)。
振动能和电子能的表达式是基于玻尔兹曼分布和双原子分子谐振子假设:
$$e^v_s=\frac{R_s \theta^v_s}{exp(\theta^v_s/T^v)-1}$$
$$e_{s}^{el}=\dfrac{(g_1/g_0)\exp (-\theta_s^{el}/T^{el})}{1+(g_1/g_0)\exp (-\theta_s^{el}T^{el})}\theta^{el}_1 R_s$$
双温模型认为$T^v=T^{el}$,并且额外考虑振动能的弛豫过程。
Model 2
另外一种热力学模型使用关于温度的多项式拟合函数来确定内能,在$300K\lt T \lt 30000K$的范围内:
$$c_{p,s}=R_s \sum_{k=0}^{4} A_{k,s}T^k$$
$$e_s=R_s \sum_{k=1}^{5} \frac{A_{k,s}}{k}T^k -R_s T + e^0_s$$
说明:
- 在单温度模型下,即仅考虑化学非平衡时,可以令Model 1中所有的温度都为一个温度。Model 2中的温度也就是这个温度。
- 对于热化学非平衡流,我暂时不清楚Model 2中的温度是什么温度,其计算的内能是否包含振动能电子能。我暂时假定Model 2仅仅利用平动旋转温度来计算包含了振动能和电子能的热容和能量。
- 电子能也有许多能级,上边公式仅仅考虑了一个能级。编程初期,我干脆忽略电子能好了。
对比
氧气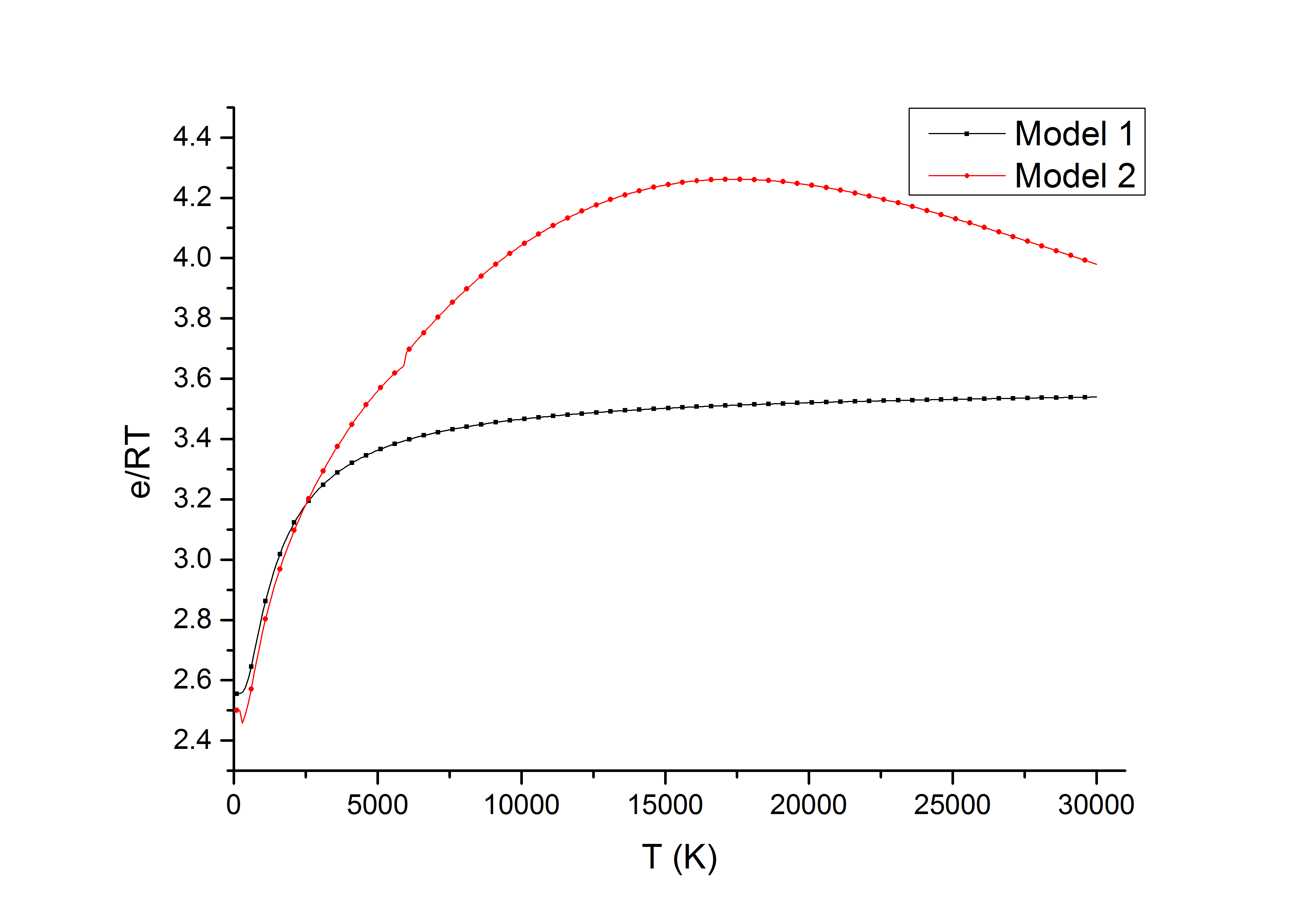
氮气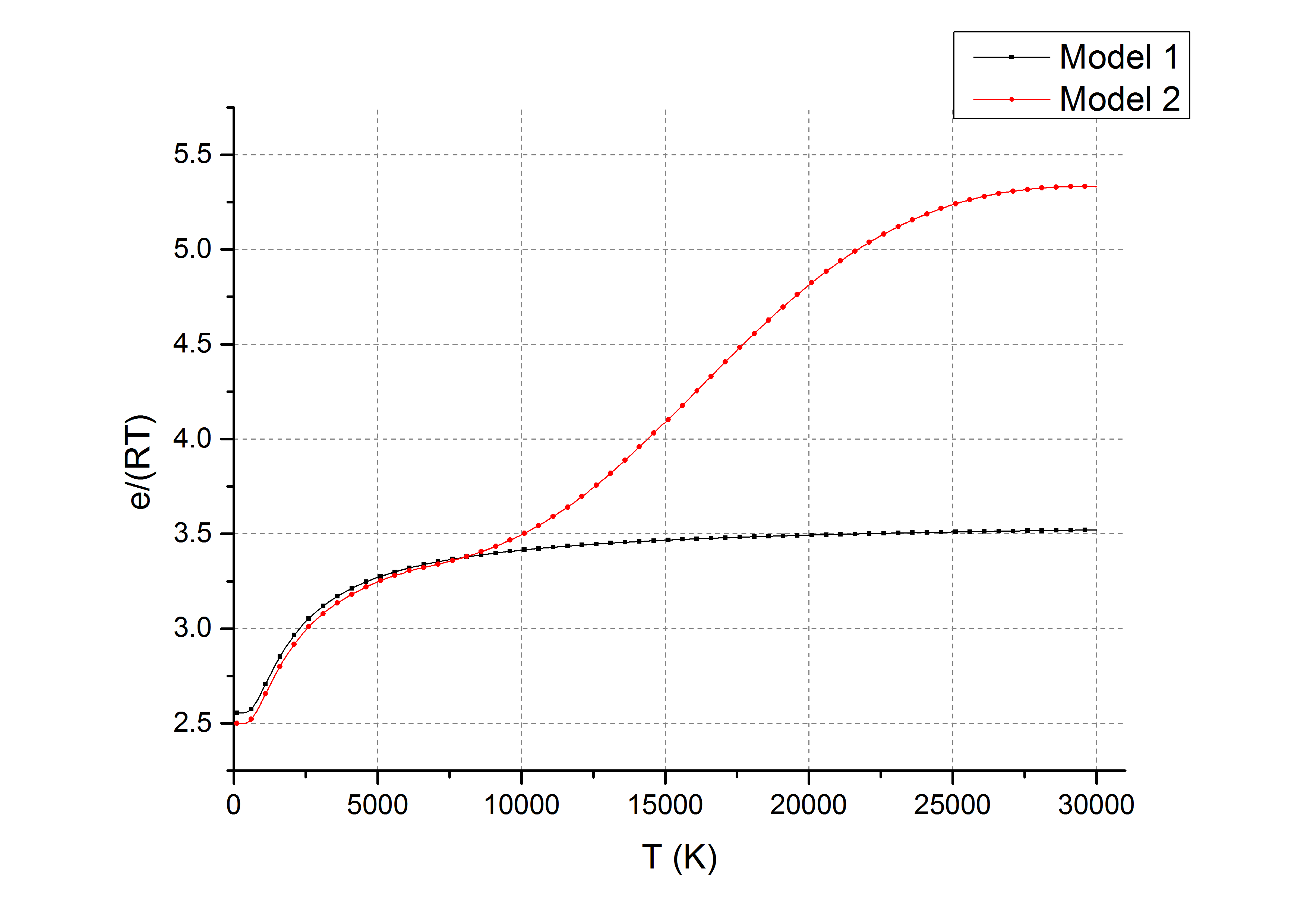
氧原子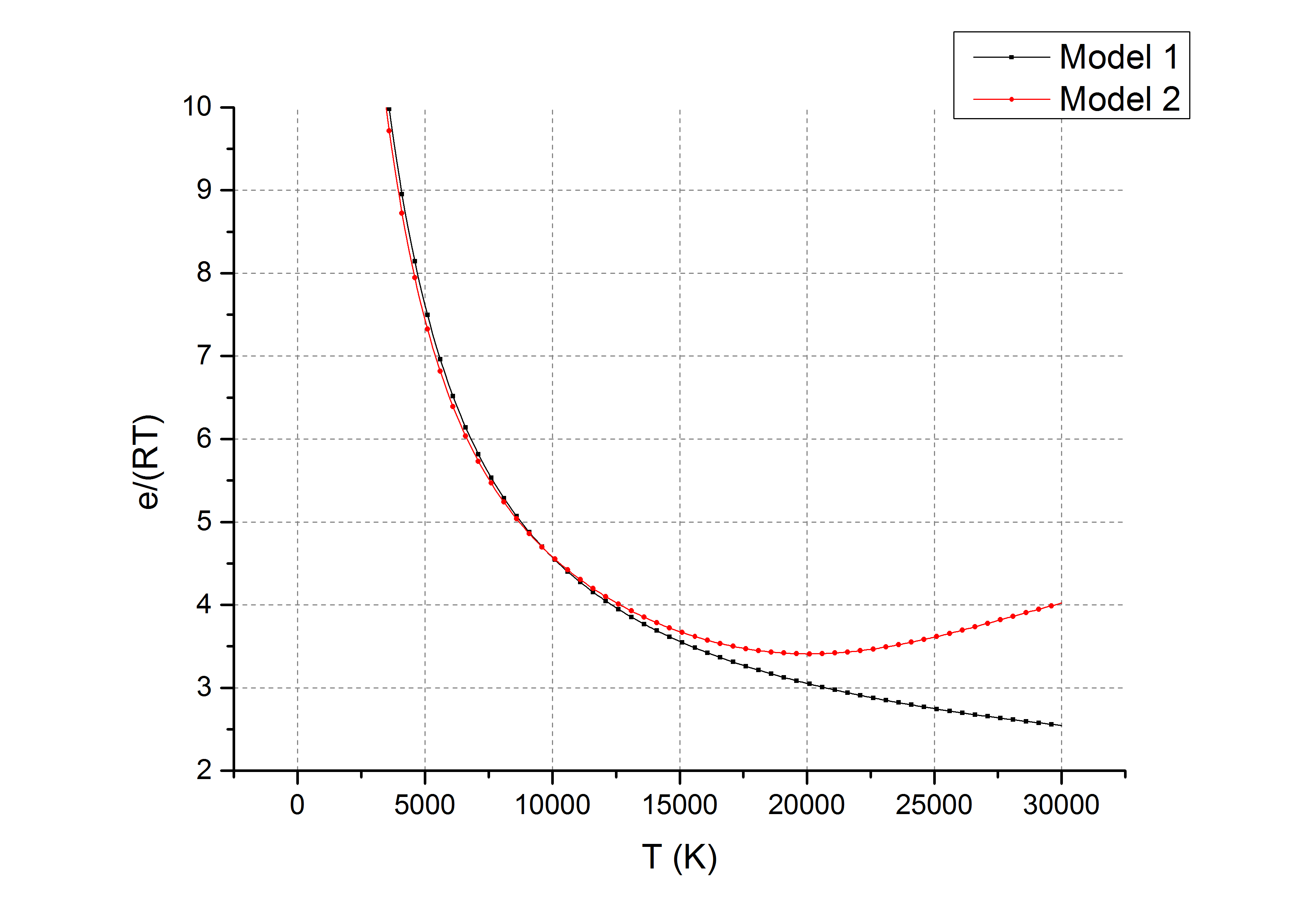
说明:
- 由于计算中Model 1 忽略了电子能,造成高温时($T>10000K$)时Model 1结果明显小于拟合结果。
- $O_2$在$6000K$时有间断,可能是数据抄错了?todo:核对叶老师程序中的数据。
- 如果考虑多级电子能,那么内能和比热容的计算过程略繁杂。
所以在编程中,为了方便,我先暂时采用Model 1,忽略电子能。等将来程序跑起来了,再使用Model 2 或者给Model 1 添加电子能。